Arbeitsfreies bzw. passives Einkommen: Renten, Erträge & Co.
Serie zum Fokus-Thema „Rente selbstgemacht“
Teil 2
Renten selbst berechnen als erster Schritt zur „Do it Yourself-Rente“
Was Sie in Teil 2 erwartet:
- Erkenntnis, dass bei passivem Einkommen ein Wertspeicher die Grundlage der Rente ist.
- Was dynamisierte Renten sind.
- Unterscheidung von vor- und nachschüssigen Renten sowie unendlichen und endlichen Renten.
- Wie Sie die Verrentung eines heute verfügbaren Kapitalbetrages berechnen.
- Wie sie den heutigen Wert = Barwert einer Rente ermitteln.
- Vorfreude auf ein kostenfreies EXCEL-Tool im Blogbeitrag am nächsten Freitag.
Was Sie in Teil 1 erfahren haben:
- Start der Tool-Box-Serie „Rente selbstgemacht“.
- Zusammenhang zwischen Renten und passivem bzw. arbeitsfreiem Einkommen.
- Renten müssen keineswegs vom Staat oder Versicherungsgesellschaften kommen.
- Die wichtige Unterscheidung zwischen Ansparphase und Rentenphase.
- Wie Sie Rentenfaktoren identifizieren, interpretieren und clever umrechnen.
- Die Tücke mit den Rentenfaktoren deutscher Lebensversicherer.
- Auslobung eines wertvollen Buches, wenn Sie einen möglichst wertlosen (niedrigen) Rentenfaktor nachweisen! Für diesen kleinen Wettbewerb berücksichtige ich Einsendungen noch bis zum 07. September 2021.
Sie wissen also bereits, dass passives Einkommen in Form von regelmäßigen – z.B. monatlichen – Zuflüssen keineswegs nur von der gesetzlichen Altersrente oder privaten Versicherungsverträgen her kommt. Und dass Rente eben auch nicht unbedingt etwas mit Alter oder Erwerbsunfähigkeit zu tun hat, sondern der gebräuchliche Ausdruck für Annuität (regelmäßiger Zahlungsstrom) ist.
Zur Sicherheit hier noch einmal die Definition von „Rente“:
Als Rente im finanzmathematischen Sinne versteht man eine Folge von Zahlungen, die über einen endlichen oder unendlichen Zeitraum hinweg
– erstens in konstanter Höhe und
– zweitens in konstantem zeitlichen Abstand
hinweg fließen.
Also beispielsweise an jedem Monatsende wiederkehrend 1.000 Euro oder jährlich am 31. Dezember 10.000 Euro.
Damit wird schon deutlich, dass der Erhalt einer Zahlung von Alters-, Invaliditäts- oder sonstigen staatlichen Renten nur einen kleinen Teil der möglichen Erscheinungsformen von Renten ausmacht.
Auch mit Pensionszahlungen, Betriebsrenten oder Renten aus privaten Vorsorgeverträgen ist die Vielfalt noch keineswegs abgedeckt. Zahlungsströme in Form von Renten liegen nämlich auch bei allen Annuitätenkrediten sowie Leasingverträgen oder Miet- und Pachtverträgen vor.
So gesehen stellt auch das Arbeitseinkommen eine Rente im finanzmathematischen Sinne dar – aber nur bis zur nächsten Gehaltserhöhung, hoffentlich 😉
Sonderfall: Dynamisierte Renten
Obwohl – wie oben definiert – die Zahlungshöhe einer Rente konstant sein soll, spricht man in der Praxis oft von „dynamisierten Renten“. Das sind Renten, die mit einer bestimmten Wachstumsrate ansteigen – also nominell eben gerade nicht konstant sind.
Dies entspringt dem Bedürfnis nach realen (also in Kaufkraft) konstanten Zahlungen. Wenn z.B. die Rentenzahlung jährlich jeweils mit 3% ansteigt, kompensiert das eine gleich hohe Inflation.
Die Rente wächst also nominal, ist aber real konstant.
Gebrauchsanweisung für nachschüssige Renten
Der Einfachheit und Praxisrelevanz halber werden alle Beispiele in diesem Beitrag auf nachschüssige Jahresrenten bezogen, d.h. die Rente kommt immer am Ende eines Jahres.
Neben nachschüssigen Renten (die also stets am Ende einer Periode fließen), gibt es auch vorschüssige Renten (zahlbar also jeweils am Periodenanfang).
Da vorschüssige Renten aber hierzulande eher selten sind (lediglich in Großbritannien vorherrschend), soll auf sie hier nicht vertiefend eingegangen werden. Das Rechentool, das ich Ihnen im nächsten Blogbeitrag überlassen werde, ermöglicht jedoch auch die bequeme Ermittlung vorschüssiger Renten 😉
Falls Sie Monatsrenten wünschen, bitte einfach durch 12 teilen und die unterjährige Verzinsung großzügig ignorieren. Das Ergebnis ist trotzdem hinreichend genau und die Musik spielt ganz sicher nicht bei der minimalen Verzinsung während des laufenden Jahres.
Unterscheidung von unendlichen und endlichen Renten
Grundsätzlich werden in der Finanzwelt unendliche und endliche Renten unterschieden.
Oben hatte ich es schon kurz angesprochen: Jede Rente, die aus einem passiven Einkommen fließt, wird aus einem Wertspeicher geschaffen. Entweder aus dessen Erträgen (unendliche Rente) oder zusätzlich auch aus dessen Substanz (endliche Rente).
Unendliche Renten können auch als Renten ohne Kapitalverzehr bzw. Renten mit Kapitalerhalt bezeichnet werden. Der Wertspeicher (also der Kapitalstock, die Substanz) wird hierbei nicht angegriffen, sondern dient als nachhaltige Quelle der periodischen Ausschüttungen.
Endliche Renten werden auch als Renten mit Kapitalverzehr bzw. Renten ohne Kapitalerhalt bezeichnet. Bei diesen Renten wird ganz bewusst auch die Substanz im Zeitablauf aufgezehrt, um eine höhere periodische Ausschüttung zu ermöglichen. Die führt – sofort erkennbar – zu einer begrenzten Laufzeit der Rente, die zwangsläufig enden muss, wenn die Basis der Ausschüttungen aufgezehrt ist.
Im Folgenden werden beide Rentenarten näher erläutert.
Unendliche Renten
Vielleicht denken Sie jetzt, dass es für unendliche Renten kaum Anwendungen gäbe.
Jedoch gibt es erstens sogenannte „Perpetuals“. Das sind tatsächlich unbegrenzt laufende Rentenzahlungen, die man erwerben, genießen, weiterverkaufen oder weitervererben kann.
Und zweitens den sehr häufigen Fall, in dem Menschen die Früchte ihrer Reserven (z.B. Dividendenzahlungen) genießen, jedoch den Kapitalstamm selbst nicht angreifen wollen.
Dieser Wunsch wird durch die Rente ohne Kapitalverzehr bzw. Rente mit Kapitalerhalt erfüllt. Sie pflücken sozusagen die Äpfel, lassen den Baum aber unangetastet.
Drittens gibt es den ebenfalls häufigen Fall, dass eine Rente zwar nicht wirklich unendlich, aber doch über sehr viele Jahre läuft. Dies ist z.B. bei Mieteinkünften aus Immobilienvermögen der Fall. In diesen Fällen wird die sogenannte unendliche Rente gerne als bequeme Annäherung für eine langjährige Rente gleicher Höhe angenommen, da die Berechnung des Wertes einer sogenannten unendlichen Rente viel einfacher ist.
Endliche Renten
Umgekehrt ist es bei endlichen Renten: Hier entnehmen Sie nicht nur die Früchte, sondern auch ein wenig Substanz. Sie verfeuern sozusagen immer ein bisschen mehr Holz des Waldes, als nachwachsen kann – also nimmt der Baumbestand allmählich ab.
Zwei Fragestellungen beim Rechnen mit Renten
Nun aber zu dem Wunsch vieler Blogleser, die Höhe ihres ganz persönlichen passiven Einkommens selbst ermitteln zu können. Oder auch den Wert von ihnen angebotenen Renten interpretieren zu können.
Dabei sind zwei unterschiedliche Fragestellungen relevant.
1. Fragestellung – Verrentung eines heute verfügbaren Kapitalbetrages
Gegenwärtig steht ein Kapitalbetrag zur Verfügung, aus dem eine Rente gebildet werden kann. Hier stellt sich meist die Frage, wie hoch und wie lange die Zahlungen aus dem vorhandenen Kapitalbetrag möglich sind. Es steht also ein heute in t0 (wobei t für die Zeit steht) vorhandener Wertspeicher zur Verfügung, aus dem über eine gewünschte Laufzeit eine Rente geschaffen werden soll.
Beispiel: Frau Reinhardt erhält eine Abfindung und will sich daraus eine Zusatzrente basteln.
2. Fragestellung – Ermittlung des heutigen Wertes = Barwertes einer Rente
Im umgekehrten Fall steht eine Rente fest, also ein Zahlungsstrom, dessen Höhe und Laufzeit bekannt sind. Hier stellt sich die Frage, wie hoch der Barwert, also der Gegenwartswert dieser Rente ist.
Dies entspricht exakt der Fragestellung, wie groß ein heute (t0) zur Verfügung stehender Kapitalbetrag sein müsste, um eine (in Höhe und Laufzeit) gewünschte Rente zu ermöglichen.
Beispiel: Herr Lang möchte ab nächstem Jahr 30 Jahre lang monatlich eine Zusatzrente von 500 Euro erhalten. Welchen Betrag (Barwert) müsste er hierfür zur Verfügung haben?
Formeln für unterschiedliche Fälle
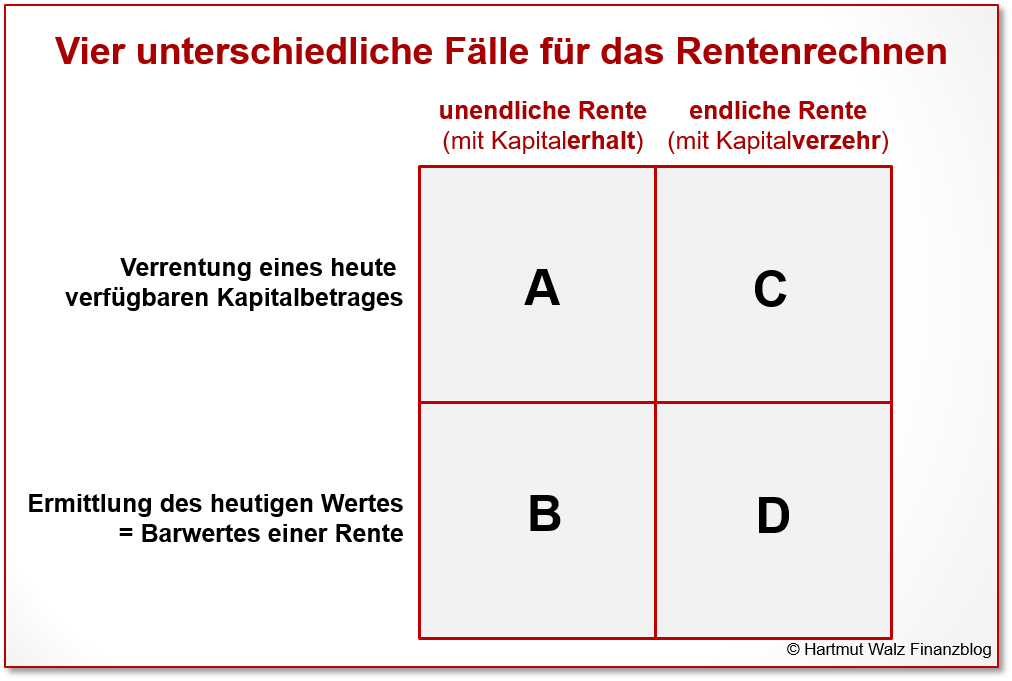
Hier kommt nun wieder die oben gemachte Unterscheidung zum Tragen, ob eine unendliche oder eine endliche Rente berechnet werden soll. Es ergibt sich also eine Matrix mit vier unterschiedlichen Fällen für das Rentenrechnen:
Die vier Fälle werden nachfolgend vorgestellt.
A) Verrentung eines Kapitalbetrages für eine unendliche Rente (Rente mit Kapitalerhalt)
Dies ist der einfachste Fall. Denn wenn das Ursprungskapital erhalten bleiben soll, dann darf nur der Ertrag daraus entnommen werden.
Bei einer erwarteten Durchschnittsverzinsung (Rendite) von R% dürfen also am Ende jedes Jahres eben nur diese R% vom Kapitalbetrag entnommen werden.
Rente = R% * Kapitalbetrag
Zwei relevante Hintergrundüberlegungen – gerade in der Nullzinswelt:
Erstens: Wird Geld in der aktuellen Situation mehr oder weniger zinslos angelegt, so bedeutet dies ganz klar, dass auch keine Entnahme stattfinden darf, wenn der Kapitalbetrag erhalten bleiben soll.
Zweitens: Orientieren Sie sich am Ziel des realen Kapitalerhalts, so sollten Sie sogar noch die Inflationsrate I% von der Durchschnittsverzinsung R% abziehen und nur die Differenz mit dem Kapitalbetrag multiplizieren.
Die Formel lautet also nun:
Rente (real) = (R% – I%) * Kapitalbetrag
Diese Vorgehensweise ist nur eine Annäherungsrechnung, aber dafür sehr einfach und hinreichend genau.
Es wird also deutlich, dass der reale Erhalt eines Kapitalbetrages nicht gelingt, wenn die Inflationsrate den erzielbaren Durchschnittszins übersteigt.
Wenn also beispielsweise bei einer möglichen Durchschnittsverzinsung von 2% p.a. die Inflation 3% p.a. beträgt, müssten Sie sogar noch jährlich Geld einbringen, um Ihr Realkapital zu erhalten.
***
Die angedeutete Problematik „reale Werte versus nominelle Werte“ gilt auch für alle nachfolgenden Fragestellungen in gleicher Weise, soll aber nicht stets wiederholt werden.
Interessieren Sie sich also für reale Renten oder reale Barwerte von Renten, so ersetzen Sie R% in den nachstehenden Formeln bitte stets durch R% – I%.
***
B) Ermittlung des Barwerts = heutigen Wertes einer unendlichen Rente (Rente mit Kapitalerhalt)
Diese Fragestellung ist interessant, wenn man eine unendliche oder sehr langjährige Rentenzahlung bewerten bzw. mit einem heutigen Kapitalbetrag vergleichbar machen möchte. Oder wenn man wissen möchte, welchen Kapitalbetrag man benötigt, um daraus dann eine gewünschte Rente ohne Kapitalverzehr (= mit Kapitalerhalt) zu erzeugen.
Die Formel lautet:
heutiger Kapitalbetrag = jährliche Rente / Zinssatz (R) in Dezimalschreibweise
Ein Beispiel:
Der Anleger strebt eine zusätzliche Rente von monatlich 833 Euro, also rund 10.000 Euro jährlich (p.a.) an. Für den zu verrentenden Kapitalbetrag erwartet er eine jährliche Rendite von (Fall I) 6% bzw. (Fall II) 2%.
Fall I: Bei 6% p.a. Renditeerwartung benötigt er einen Kapitalbetrag von 166.667 Euro (errechnet aus: 10.000 Euro / 0,06) um die Wunschrente ohne Kapitalverzehr zu erzeugen.
Fall II: Bei nur 2% p.a. sind es hingegen bereits 500.000 Euro (nämlich: 10.000 Euro / 0,02).
Bitte beachten Sie, diese Rechnung berücksichtigt keinen Inflationsausgleich! Siehe rote Anmerkung oben.
C) Verrentung eines Kapitalbetrages für eine endliche Rente (Rente mit Kapitalverzehr)
In den Fällen endlicher Renten wird die Laufzeit der gewünschten Rente relevant, da ja der Kapitalverzehr des ursprünglichen Kapitalbetrags über die Laufzeit zur Erhöhung der Rente verwendet werden darf.
Daher kann der Entscheider eine Festlegung der gewünschten Rentendauer (Laufzeit in Jahren) treffen. In der folgenden Formel ist diese mit n einzusetzen und ergibt den sogenannten Annuitätenfaktor.
Ein Beispiel, angelehnt an die Zahlen von oben: Ein mit einer Durchschnittsrendite von 2% p.a. angelegter Kapitalbetrag von 500.000 Euro darf in die nächsten 30 Jahre aufgezehrt werden.
Der Annuitätenfaktor errechnet sich aus 0,02 * 1,0230 / (1,0230 -1), also 0,036227 / 0,811362 = 0,04465 oder 4,465%. Das heißt, dass 500.000 Euro * 0,04465, also 22.325 Euro jährlich über die 30jährige Laufzeit entnommen werden können.
D) Ermittlung des Barwerts = heutigen Wertes einer endlichen Rente (Rente mit Kapitalverzehr)
Hierzu benötigen Sie den Rentenbarwertfaktor, der ganz einfach der Kehrwert des o.g. Annuitätenfaktors ist 😉
Lassen Sie uns das obige Beispiel als Test gegenrechnen: Der Kehrwert von 0,04465 (siehe oben) oder direkt aus der vorgenannten Formel errechnet, beträgt 22,3964. Multipliziert man 22.325 Euro jährliche Rente mit diesem Faktor, ergeben sich wieder die 500.000 Euro.
Nun sind Sie also in der Lage, alle Fragestellungen rund um Rente selbst zu rechnen – eine ideale Voraussetzung für mündige Selbstentscheider.
Und was bedeutet das nun konkret für Sie?
-
Sie können mit Hilfe der obigen Formeln heutige Kapitalbeträge in Renten gewünschter Laufzeit umrechnen oder überprüfen, welche Rente Sie benötigen, um einen angemessenen Gegenwert für Ihren Kapitalbetrag zu erhalten.
-
Sie können mit Hilfe der obigen Formeln unschwer heutige Kapitalbeträge in Renten gewünschter Laufzeit umrechnen oder überprüfen, welche Rente Sie benötigen, um einen angemessenen Gegenwert für Ihren Kapitalbetrag zu erhalten.
-
Und Sie können umgekehrt den Barwert = Gegenwartswert einer Ihnen angebotenen Rente ermitteln bzw. können ermitteln, welchen Kapitalbetrag Sie benötigen, um daraus dann eine gewünschte Rente zu erzeugen.
-
Wenn Sie die innere Logik erst einmal verstanden haben, können Sie die Arbeit dem praktischen EXCEL-Tool überlassen, das ich Ihnen zur kostenlosen Nutzung im nächsten Blogbeitrag zur Verfügung stelle.
- Außerdem können Sie die ermittelten Zahlen interpretieren und so z.B. feststellen, wie viele Jahre eine Ihnen angebotene Rente mindestens fließen müsste, um einen Ihnen alternativ angebotenen Kapitalbetrag heute zu übersteigen.
- Solche Alternativbetrachtungen machen Sie fit und entscheidungsfähig bei einer Vielzahl von Fragestellungen. Zum Beispiel wenn Ihnen ein Finanzdienstleister die Verrentung einer Ablaufleistung anbietet (dann können Sie nämlich selbst unschwer errechnen, wie alt sie werden müssen, damit sich das Angebot lohnt).
- Somit haben Sie die Kompetenz, unvorteilhafte Angebote identifizieren und aussortieren zu können.
- Man muss kein Prophet sein, um vorhersagen zu können, dass fast alle Blogleser nach der Lektüre dieses Beitrags von einer Versicherungsrente Abstand nehmen – sofern sie das können und nicht einem Verrentungszwang unterliegen (wie z.B. bei Riester- und Rürup-Verträgen).
Im Folgebeitrag am nächsten Freitag erhalten Sie eine sehr bequeme Gebrauchsanleitung und ein paar Anwendungsfälle rund um eine EXCEL-Kalkulationshilfe für praktische Fragestellungen rund um Renten.
Ich hoffe, Sie stimmen mir zu: Rentenrechnen ist gar nicht so schwer – und kann äußerst nützlich sein. Oder?
Bitte diesen Blogbeitrag weiterempfehlen – und auf das EXCEL-Geschenk nächsten Freitag freuen 😉
Herzliche Grüße
Hartmut Walz
Sei kein LeO!
Erschienen am 20. September 2021.
Der Hartmut Walz Finanzblog ist unabhängig, kosten- und werbefrei. Ich erhalte für Links und Empfehlungen keinerlei Honorar, Kick-back, Beteiligung o. ä.






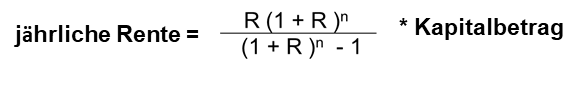
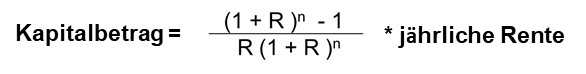

Lieber Hr. Walz,
vielen Dank für ihre Schritt-für-Schritt Anleitung!
Vor einiger Zeit habe ich für mich die Fälle C und D gerechnet. Dabei habe ich als Annahme die Verzinsung der Inflation gleichgesetzt. Die Formel wird dadurch noch einfacher, nämlich Jährliche Rente = Kapitalbetrag / Jahre. Sozusagen nebenbei erhält man die jährliche Rente sogar als „abgezinsten Realwert“ bzw. kann die nominelle jährliche Rente mit dem Zinsatz / Inflationsrate als Realwert umrechnen.
Ich frage mich allerdings, ob ich mich während der Ansparphase bereits zwischen endlicher und unendlicher Rente entscheiden muss bzw. sollte, beispielsweise durch kauf eines thesaurierenden vs. eines ausschüttenden ETFs (ggfs. plus eigenständige Reinvestition der ausgeschütteten Gewinne)?
Theoretisch ließe sich ein thesaurierende ETF zu Rentenbeginn verkaufen und von dem Erlös ein ausschüttender ETF kaufen, aber als guter Deutscher möchte man das ganze ja gerne im Hinblick auf die Steuern optimieren…
Lieber Sebastian, ich schätze Ihren Kommentar und auch die verschiedenen fachlichen Überlegungen sehr. Jedoch kann ich nicht allen Gedanken von Ihnen folgen…
Ganz unabhängig davon, wie Sie Ihre Lebenserwartung und Ihre Entnahmewünsche in der Rentenphase sehen und planen, ist Ihre Ansparphase auf alle Fälle endlich. Und somit die Wahl eines Rentenfaktors auf begrenzte Laufzeit eine eindeutige und nicht zu diskutierende Entscheidung.
Die von Ihnen hergestellte Verbindung der Fragestellung „ausschüttend vs. thesaurierend“ kann ich ebenso nicht nachvollziehen, da sich die Entscheidung hierüber aus ganz anderen Überlegungen heraus als Rentenfaktoren oder Restlebenserwartung ableiten sollte.
Letztlich ist für die Entscheidung zwischen Ausschüttung und Thesaurierung vor allem die Entwicklung künftiger Steuersätze auf Kapitaleinkünfte relevant und da ich möglichst prognosefrei arbeite, möchte ich mich in diese emotionale Diskussion nicht einschalten 😉
Viele herzliche Grüße und weiterhin alles Gute für Sie
Hartmut Walz – Sei kein LeO!
Lieber Hr. Walz,
meine Rechnung ginge beispielsweise so: Gewünscht ist eine jährliche (endliche) Rente von 20.000€ (real) über 30 Jahre. Durch Multiplikation erhalte ich den benötigten Betrag von 600.000€.
Im ersten Jahr habe ich also 600.000€, entnehme 20.000€, die restlichen 580.000€ verzinsen sich z.B. mit 3%.
Im zweiten Jahr habe ich somit 597.400€ (580.000*1,03), davon entnehme ich 20.600€ (20.000 *1,03). So habe ich die 3% Inflation ausgeglichen, habe also real die selbe Kaufkraft wie im Jahr zuvor mit den 20.000€.
Nach 30 Jahren wäre mein Kapital verbraucht bei real gleichbleibender Rente, solange eben die Verzinsung der Inflation entspricht.
Einen Rentenfaktor brauche ich für diese Rechnung nicht (wüsste auch nicht wie ich den aufgrund der nominell steigenden Rentenbeträge errechnen müsste).
Über potenziell enthaltene Denk- oder Rechenfehler lasse ich mich gerne aufklären.
Lieber Sebastian, danke für Ihre Erläuterung. Jetzt verstehe ich Ihren Denkansatz, der auf Basis Ihrer Annahmen auch korrekt ist.
Als Orientierung ist das prima. In der Praxis treten Risiken eben dadurch auf, dass die Verzinsung nicht mit der Inflationsrate übereinstimmt. Es gibt eine umfangreiche und kleinteilige Literatur zu dieser Problematik, die ich Ihnen an dieser Stelle aber nicht zumuten möchte (Schlagwort: Sequence of Returns – Risk) 😉
Herzliche Grüße, Hartmut Walz – Sei kein LeO!
Guter Artikel, man ist schon gespannt auf den nächsten Teil. Schön wäre, wenn man auch Tipps zur sicheren Entnahmerate eines breit diversifizierten Portfolios geben könnte. Das wird für viele das größte Problem sein.
Das wäre auch ein schönes Thema für ein paar YouTube-Videos.
Gruß H.
Ja, liebe/r H., man könnte noch so viel machen… 😉
Herzliche Grüße, Hartmut Walz – Sei kein LeO!
Vielen Dank für den hilfreichen und verständlichen Blogbeitrag.
Ich kann mir einen fünften Fall vorstellen. Es geht um eine endliche Rente mit Kapitalverzehr. Gegeben sei das zu verrentende Kapital, die jährliche Rente und die Durchschnittsverzinsung. Gesucht ist die Laufzeit der Rente. Vielleicht ist dieser Fall auch von allgemeinen Interesse.
Mit freundlichen Grüßen, Klaus Göbel
Lieber Klaus Göbel, herzlichen Dank für Ihren Kommentar und die Anregung.
Die von Ihnen gewünschte Konstellation habe ich sofort verstanden und verspreche Ihnen, dass ich darauf in einem der nächsten Blogbeiträge eingehen werde. Und zwar so, dass Sie das Beispiel ganz einfach auf Ihre konkrete Situation umrechnen können.
Versprochen! 😉
Herzliche Grüße, Hartmut Walz – Sei kein LeO!
Bei der Ermittlung des Barwertes zugunsten einer langjährigen Zahlungsreihe in der heutigen Nullzinswelt, wird m.E. auch deutlich, warum man im Jahr 2018 die Arbeitgeberhaftung für Bruttoentgeltumwandlungen im Zuges des Betriebsrentenstärkungsgesetzes „sicherheitshalber“ aufgeweicht hat…
Freundliche Grüße
Philipp Hansert
Lieber Philipp Hansert, danke für diesen scharfsinnigen Kommentar. Tja – ein Schalk, wer Böses dabei denkt… 😉
Ich würde Ihnen ja so gerne widersprechen – wenn ich nur ein Gegenargument hätte…
Herzliche Grüße, Hartmut Walz – Sei kein LeO!
Ganz herzlichen Dank!
Vor allem für die praktischen, anschaulichen Beispiele im Anschluss an die Formeln.
Ihre Rentenreihe kommt wie gerufen : )
Liebe Elisabeth, das höre ich gerne! 😉
Bitte weitersagen.
Herzliche Grüße, Hartmut Walz – Sei kein LeO!
Lieber Herr Prof. Walz, herzlichen Dank für diesen tollen Artikel, der vielen Leserinnen und Lesern dabei hilft, mündig und reflektiert finanzielle Entscheidungen zu treffen! Ich freue mich schon auf das Excel-Tool!
Liebe/r Teamgeit, das ist der Plan – Hilfe zur Selbsthilfe! 😉
Herzliche Grüße, Hartmut Walz – Sei kein LeO!
Es freut mich, hier als erster kommentieren zu dürfen. Vielen Dank für die anschauliche Erklärung. Das macht es auch vielen Bekannten von mir einfacher, die Dringlichkeit der eigenen Rentenvorsorge zu verstehen. Das Excel-Tool wird sicher sehr sinnvoll sein.
Vielen Dank, für die Zeit die Sie in diese Blogartikel investieren Prof. Walz!
Lieber Samuel, es freut mich, wenn Sie und Ihre Bekannten die Dringlichkeit der eigenen Altersvorsorge verstehen – und damti einen „Griff zum Anpacken“ erhalten. So soll es sein! 😉
Herzliche Grüße, Hartmut Walz – Sei kein LeO!
Der Barwert des Textes nach Steuer und Inflation geht gegen unendlich. Auch bei der endlichen Rente. Vielen Dank!
Lieber Raimund Gebhardt, so ein toller Kommentar! ;-D
Vielen Dank!
Herzliche Grüße, Hartmut Walz – Sei kein LeO!